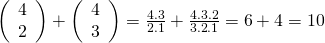( n kombinasyon kuralları ) elemanlı bir kümenin ( r ) elemanlı kombinasyonu ( C(n, r) ) ya da ( binom{n}{r} ) ile gösterilir ve aşağıdaki formülle hesaplanır. ( binom{9}{0} = binom{9}{9} ), ( binom{9}{1} = binom{9}{8} ), ( binom{9}{2} = binom{9}{7} ), ( binom{9}{3} = binom{9}{6} ), ( binom{9}{4} = binom{9}{5} ) olur.
Smm Panel Scripti Satın Al

Çizeceğimiz doğrunun bu 5 noktadan herhangi 2 tanesinden geçmesi istendiği için bu 5 noktadan 2 tanesini seçeriz. Not: Permütasyonda sıralama önemli iken, Kombinasyonda sıralama önemli değildir.
( binom{79}{r^2 + 1} - binom{79}{r + 6} = binom{79}{r + 7} - binom{79}{r^2} ) olduğuna göre,. ( C(8, 3 C(8, 4 C(9, 4) ). kombinasyon kuralları “Geometrik Diziler” konusuna ait soruların çözümleri video olarak eklenmiştir. (21/12/2022). Permütasyon ve kombinasyon formülleri aşağıdaki gibidir.
Dfrac{n!}{(n - r)!} = P(n, r) kombinasyon kuralları ). Örnek: eşit midir? İnceleyelim.
Dopingbet Casino

( A )'nın 1'li Kombinasyonları: ( {a}, {b}, {c}, {d}, {e} ). ( C(n, 0 C(n, 1 C(n, 2 ldots ) C(n, n - 1 C(n, n) ) 2^n kombinasyon kuralları ).
kombinasyon kuralları ( n, r in mathbb{N}, quad r le n ) olmak üzere,. 5A) Bu beş noktanın herhangi ikisinden geçen kaç farklı doğru çizilebilir?. Buna göre ( x )'in alabileceği değerler toplamı ( 5 + 3 = 8 ) olur.
Bağkur 13 Ek 63 Terki
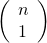
( A = { 1, 2, 3, 4, 5 } ) olmak üzere,. Alt kümenin üç elemanından ikisinin “S” ve “E” olmasını istediğimiz için “S”yi ve “E”yi eleman olarak alırız, diğer bir elemanı kombinasyon kuralları {L, A, M} arasından seçeriz. ( B ) kümesinin 2'li kombinasyonları: ( {ext{Eda}, ext{Ela}}, {ext{Eda}, ext{Can}}, ) ( {ext{Eda}, ext{Cem}}, {ext{Ela}, ext{Can}}, ) ( {ext{Ela}, ext{Cem}}, {ext{Can}, ext{Cem}} ).
ÖRNEK 4: A = { S, kombinasyon kuralları E, L, A, M } kümesinin 3 elemanlı alt kümelerinin;.
Golvar Canlı Yayın

Cevabı C (5, 2 10 olarak buluruz. ( C(100, 60 C(100, 40) ). (binom{22}{3} (frac{22!}{(22-3)!. 3!} (frac{22!}{19!. ( C(n, 1 C(n, 3 C(n, 5 ldots = 2^{n - 1} ). kombinasyon kuralları N ve r birer doğal sayı ve r ≤ n olmak üzere n elemanlı bir kümenin r elemanlı alt kümelerinin her birine n’nin r’li kombinasyonu denir.
KOMBİNASYON SAYISI
( C(n, n - 1 2 cdot C(n, n - 2 100 ) eşitliğini sağlayan ( n ) doğal sayısı kaçtır?. ( P(5, 3 C(5, 3) cdot 3! ). Üçgenin 2 köşesinin d1 üzerinde, 1 köşesinin d2 üzerinde olması durumunda (binom{4}{2} (binom{6}{1} 6. 6 = 36 üçgen çizilebilir.
( binom{80}{r^2 + 1} = binom{80}{r + 7} ). ( n ) elemanlı bir kümenin ( 0 )'lı ve ( n )'li kombinasyon kuralları kombinasyonları 1'e eşittir. ( n ) elemanlı bir küme içinden seçilebilecek 0 elemanlı tek alt küme boş kümedir. Boş kümenin boş küme olan alt küme sayısı 1'dir.
Hemogram Rbc Nedir